1) Θ Notation: The theta notation bounds a functions from above and below, so it defines exact asymptotic behavior.
A simple way to get Theta notation of an expression is to drop low order terms and ignore leading constants.

For a given function g(n), we denote Θ(g(n)) is following set of functions.

Θ(g(n)) = {f(n): there exist positive constants c1, c2 and n0 such that 0 <= c1*g(n) <= f(n) <= c2*g(n) for all n >= n0}

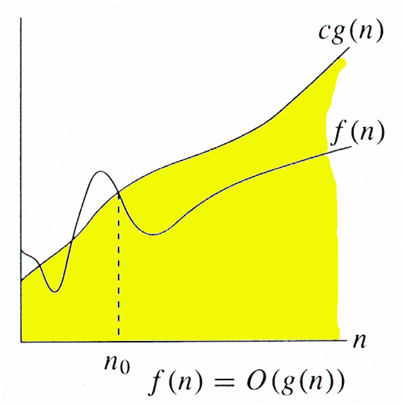
2) Big O Notation: The Big O notation defines an upper bound of an algorithm, it bounds a function only from above.

The Big O notation is useful when we only have upper bound on time complexity of an algorithm. Many times we easily find an upper bound by simply looking at the algorithm.

O(g(n)) = { f(n): there exist positive constants c and n0 such that 0 <= f(n) <= cg(n) for all n >= n0}

3) Ω Notation: Just as Big O notation provides an asymptotic upper bound on a function, Ω notation provides an asymptotic lower bound.

For a given function g(n), we denote by Ω(g(n)) the set of functions.

Ω (g(n)) = {f(n): there exist positive constants c and n0 such that 0 <= cg(n) <= f(n) for all n >= n0}.